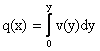Metode til bestemmelse af vandføring og tværsnitsareal
I følgende afsnit beskrives grundlaget for beregning af tværsnitsareal og
vandføring i Østerå, ud fra opmålingerne foretaget den 3. september 2003.
Det samlede tværsnitsareal er
udregnet vha. følgende formel:
hvor
n: Antal nedstik
[-]
b: Afstanden
mellem hvert nedstik [m]
y: Dybden af det
pågældende nedstik [m]
Vandhastigheden blev målt
vha. en vingehastighedsmåler, af mærket Ottflügel, i 10 centimeters interval
fra bunden og til vandoverfalden.

Figur 1 Vingehastighedsmåler med omdrejningstæller
For at finde den samlede
vandføring, Q, integreres over dybden, og dermed fås vandføringen som funktion
af tværsnitsbredden (arealhastighed).
Arealhastigheden q findes som:
hvor
x: Afstand fra brinken
[m]
v: Hastigheden [m/s]
y: Vanddybden [m]
På differensform kan
arealhastigheden udstykkes vha. trapezintegration:
(3) ![]()
hvor
n: Antal målte hastigheder
[-]
qi: Arealhastighed
[m2/s]
Den samlede vandføring kan
findes ud fra formlen:
(4) 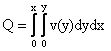
hvor
x: Tværsnitsbredden
[m]
y: Lokal
vanddybde [m]
v(y): Hastighed som
funktion af vanddybden [m/s]
Anvendes arealhastigheden
udtrykkes den samlede vandføring på differensform som:
(5) ![]()
hvor
xj: Afstand
fra bredden ud til nedstik nr. j [m]
Omregning af målt tværsnitsprofil til trapeztværsnit
I følgende afsnit beskrives formelgrundlaget for bestemmelse af trapeztværsnit
ud fra det målte tværsnit. Det teoretiske trapeztværsnit er vist på figur
2

Figur 2 Trapeztværsnit
Bundbredden, b0 estimeres
visuelt og herefter beregnes anlæggene vha. lineær regression.
Den naturlige dybde i vandløbet
findes iterativt vha. Manningformlen, hvor den naturlige dybde, y indgår både
i hydraulisk radius, R og i tværsnitsarealet, A
(6) ![]()
Hvor
M: Manningtal
I: Bundhældning
Tværsnitsarealet af trapeztværsnittet
udtrykkes vha. følgende formel:
(7) ![]()
Hvor
y: Naturlig dybde
av: Anlæg i venstre side af vandløbet
ah: Anlæg i højre side af vandløbet
Den våde perimeter, P udtrykkes
ved:
![]()
Den våde perimeter indgår i den
hydrauliske radius, R = A/P.