Diskretisering af Darcy's ligning
Til bestemmelse af grundvandsstrømningen er Darcy's ligning opsat og indsat i kontinuitetsligningen, hvormed den styrende ligning for grundvandsstrømningen er fremkommet. Der er opsat ligninger for celler syv forskellige steder i beregningsnettet. Ved klik på de enkelte situationer på ovenstående figur, fås opstilling af Darcy's ligning i kontinuitetsligningen for den valgte situation.

Darcy's ligning:

hvor	q er flowet [m3/s] K er konduktiviteten [m/s] A er det gennemstrømmede areal [m2] dh/dx er trykgradienten [-]

Kontinuitetsligningen:

hvor	Dm er magasineringen [m3/s] qind er flowet ind i den betragtede celle [m3/s] qud er flowet ud af den betragtede celle [m3/s]

Ligningerne er diskretiseret og efterfølgende løst numerisk. Diskretiseringen er udført efter princippet vist i nedenstående figur. Indekseringen er udført så x og y angiver den flade, der betragtes, og i denne sammenhæng angiver i og u, om der ses på flow hhv. ind eller ud af boksen. Til angivelse af hvilken boks der betragtes, er der anvendt indeksene i og j. i,j angiver den boks, der er taget udgangspunkt i. Boksene hhv. til højre for og over den boks der er taget udgangspunkt i, er indekseret med hhv. i+1,j og i,j+1, og boksene til venstre for og under den boks, der er taget udgangspunkt i, er indekseret med i-1,j og i,j-1.

Der er efterfølgende opsat kontinuitetsligninger ved to situationer, hhv. fyldte og delvis fyldte celler, hvori Darcy's ligning er indsat.
Ud fra ovenstående figur er der opstillet følgende diskretiseringer af Darcy's ligning ved fyldte celler:

hvor	q K dx dy h	er flowet [m3/s] er konduktiviteten [m/s] er boksstørrelsen i x-retningen [m] er boksstørrelsen i y-retningen [m] er trykniveauet [m]

Delfyldte celler

Når cellerne ikke er fyldte, sættes dy lig med dy_effektiv

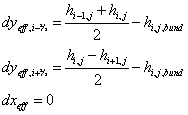
hvor	dxeff dyeff hi,j,bund	er den effektive boksstørrelse i x-retningen [m] er den effektive boksstørrelse i y-retningen [m] er trykniveauet ved boksens bund [m]

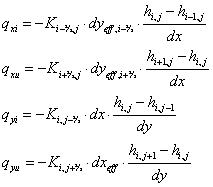
Når cellerne er delfyldte, sættes dy lig med dy_effektiv, og for flow ud af cellerne i y-retningen, q_y,u, sættes dx lig med dx_effektiv. dy_effektiv angiver højden af den del af boksen, hvor der er vandfyldt.

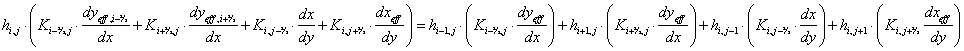hvor

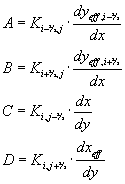Løsningen af differensligningerne sker gennem en Gauss-Seidel-iteration.