|
|
|
Figur 65 Beregnet forskydningsspændinger som funktion af vanddybden. |
Der er arbejdet med måling og beregning af forskellige strømningsmæssige parametre. I det følgende præsenteres og kommenteres de enkelte resultater. Alle parametre er bestemt med udgangspunkt i forsøgsopstillingen, hvor der er udlagt skærver i bunden af strømrenden.
Der er arbejdet med bestemmelse af bundforskydningsspændingen gennem tre forskellige metoder. Den første metode tager udgangspunkt i en kraftligevægt, hvor energiliniegradienten benyttes. Dette har dog vist sig ikke at være muligt ved den anvendte forsøgsopstilling. Den anden metode benytter friktionshastigheden, som beregnes ud fra de målte hastighedsprofiler og det empiriske udtryk for det logaritmiske hastighedsprofil. Den sidste metode tager udgangspunkt i indirekte målinger af Reynolds' spændingerne, som forlænges til bunden for en bestemmelse af bundforskydningsspændingen.
Der er benyttet to strømhastigheder, hhv. lav og høj hastighed. I nedenstående tabel ses resultaterne af de to bestemmelser.
| Tabel 6 Resultat af bestemmelse af bundforskydningsspænding ved friktionshastigheden og Reynolds' spændinger. | ||||
| Enhed | Måling 1 lav hastighed | Måling 2 høj hastighed | ||
| Bundforskydningsspænding v. friktionshastighed | t0,1 | N/m2 | 0,15 | 0,80 |
| Bundforskydningsspænding v. Reynolds' spændinger | t0,2 | N/m2 | 0,14 | 0,22 |
Ved den høje strømhastighed er der i renden også en større vanddybde end ved den
lave strømhastighed. Derfor er der, som forventet, også fundet de største
bundforskydningsspændinger ved høj strømhastighed. Der ses desuden god
overensstemmelse mellem de to metoder ved lav strømhastighed, mens der er en
større afvigelse ved den høje strømhastighed. Det er svært at fastlægge grunden
til denne afvigelse på baggrund af kun to udførte målinger. En mulighed er en
fejlmåling ved bestemmelse af Reynolds' spændingerne. Her er en enkelt
fejlmåling nok til, at den indlagte rette linje drejes, så der eksempelvis
findes en for lav værdi for bundforskydningsspændingen. En gentagelse af
forsøget, med udførelse af et større antal målinger, vil evt. kunne afgøre om
dette er tilfældet.
Som en del af bestemmelsen af bundforskydningsspænding ved friktionshastighed, er der fundet værdier for den ækvivalente sandruhed. Der er også her benyttet de to strømhastigheder i forsøgsopstillingen med skærvebund, og der er bestemt en værdi for ruheden ved begge målinger uafhængigt af hinanden.
| Tabel 7 Resultat af bestemmelse af ækvivalent sandruhed ved hhv. lav og høj strømhastighed. | ||||
| Enhed | Måling 1 lav hastighed | Måling 2 høj hastighed | ||
| Ækvivalent sandruhed | k | m | 0,14 | 0,13 |
Det ses, at to uafhængige målinger tilnærmelsesvis giver samme resultat, hvorfor
resultatet vurderes som korrekt. Sammenlignes med litteraturværdier, findes
værdier for kanal i jord at ligge i intervallet 0,01-0,2 m [Brorsen og Larsen, 2001], hvor indenfor
de fundne værdier ligger.
Begrebet sandruhed stammer fra de oprindelige forsøg med hydraulisk ru rør, som blev udført af Nikuradse ved at påføre et hydraulisk glat rør et enkelt tætsiddende lag sandkorn med veldefineret korndiameter. Med udgangspunkt i disse forsøg fremkom det empiriske udtryk for det logaritmiske hastighedsprofil, som i dette projekt er benyttet ved bestemmelse af sandruheden. Det betyder, at den her fundne sandruhed svarer til den korndiameter, der i Nikuradse's forsøg ville give samme strømningsmodstand som den faktiske overflade med skærvebund benyttet i dette forsøg. Den fundne ækvivalente sandruhed er derfor ikke en afstand, der umiddelbart kan sammenlignes med størrelsen af de ilagte skærver.
De turbulente forskydningsspændinger, også kaldet Reynolds spændingerne, er målt indirekte ned gennem profilet, for herigennem at bestemme bundforskydningsspændingerne. I nedenstående figur ses resultatet, hvor Reynolds spændingerne er vist for de to strømhastigheder.
|
|
|
Figur 65 Beregnet forskydningsspændinger som funktion af vanddybden. |
Reynolds' spændingerne udtrykker den forskydningsspænding, der forårsages af den
udveksling af bevægelsesmængde, der sker som følge af fluktuationerne på tværs
af middelstrømningen. Det ses som følge heraf, at en forøget middelhastighed
også giver en forøgelse i størrelsen på fluktuationerne, og dermed større
Reynolds spændinger. Dette er gældende i den nederste del af profilet, hvor
strømning er mest påvirket af skærvebunden.
Som den ene del af energibalancen for den betragtede strømning er den kinetiske energi betragtet ved hhv. lav og høj hastighed, og beregnet med udgangspunkt i fluktuationerne i hhv. x-, y-, og z-aksens retning og middelhastigheden. Der er skelnet mellem den turbulente kinetiske energi, som alene findes på baggrund af fluktuationerne og den totale kinetiske energi, der findes som summen af energien som følge af middelstrømningen og den turbulente kinetiske energi. I nedenstående figur ses resultatet vist som både turbulent- og total kinetisk energi for hhv. lav (måling 1) og høj (måling 2) strømhastighed.
|
|
| Figur 66 Beregnet turbulent- og total kinetisk energi for de to situationer med hhv. høj og lav hastighed. |
Den kinetiske energi dannes som følge af forskydningsspændingernes arbejde.
Betragtes de beregnede Reynolds spændinger, er det derfor forventeligt, at den
turbulente kinetiske energi er størst tæt ved bunden, samt at en forøget
strømhastighed giver en forøgelse i den turbulente kinetiske energi. Ved den
totale kinetiske energi er middelstrømhastigheden dog så dominerende, at
fordelingen ned gennem profilet har form efter det målte hastighedsprofil.
Som den anden del af energibalance er der arbejdet med bestemmelsen af dissipationen. Mens der ved forskydningsspændingernes arbejde dannes kinetisk energi, sker der en overførsel af energi til stadig mindre og mindre hvirvler, hvor der til sidst i de mindste hvirvler sker en dissipation, hvor energien omdannes til varme. Resultatet ses i nedenstående figur.
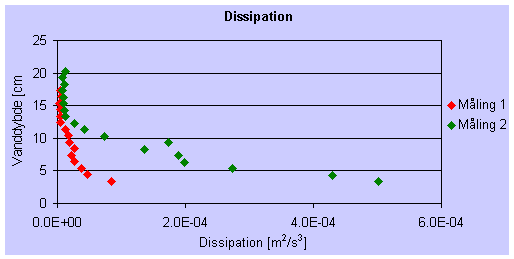 |
| Figur 67 Dissipation bestemt ved lav (måling 1) og høj (måling 2) hastighed. |
Den største dissipation ses tættest ved bunden, hvor de største Reynolds'
spændinger og den største turbulente kinetiske energi også ses. Det bemærkes
desuden, hvordan der i den øverste del af profilet, hvor der kun var en lille
turbulent kinetisk energi, ligeledes kun sker en lille dissipation. Ved en
sammenligning med litteraturen, ses samme fordeling af dissipationen i en
turbulent strømning, med de største værdier tættest ved bunden, og faldende
værdier op gennem profilet.