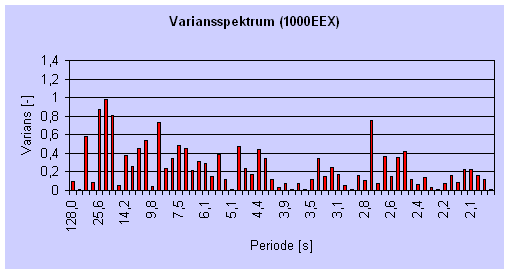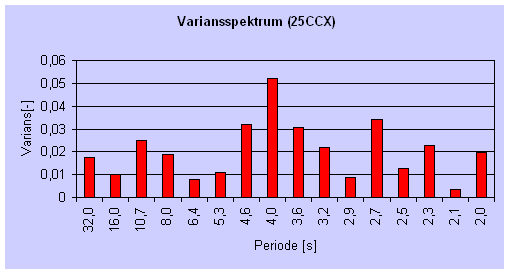
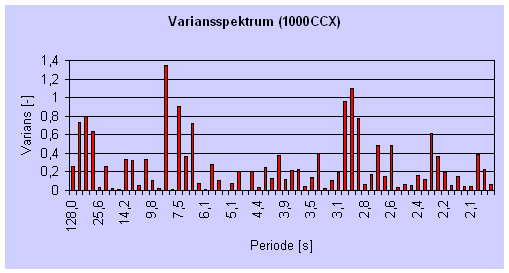
Variansspektre

I et system som det betragtede kan der være flere harmoniske svingninger, som kan påvirke målingerne. F.eks. kan der være en bølge, der løber frem og tilbage mellem rendens ender. Der kan også være en svingning i den vandføring, pumpen yder, hvilket blev observeret ved meget høje vandføringer. En model, der opstilles for at modellere forholdene, kan tilpasses bedre til de målte værdier, hvis disse svingninger kendes og medtages i modellen.
For at undersøge om der er harmoniske svingninger i tidsserien, optegnes et variansspektrum. Princippet i variansspektret er, at tidsserien omskrives til en Fourierrække. En Fourierrække kan betragtes som en summation af et uendeligt antal harmoniske svingninger med forskellig frekvens. Derfor kan denne fourier-analyse benyttes til at finde ud af, om der er nogle svingninger, der er mere fremtrædende end andre i tidsserien. På nedenstående figurer ses variansspektrene for de tre tidsserier (Excelberegning).

Figur 64 Variansspektra for de tre tidsserier.

For punkt 25CCX er tidsserien reelt for kort til, at der kan uddrages noget af den, men for de to øvrige ses det, at der ikke er nogen svingning, der dominerer dataserien. Der er nogle små ansamlinger ved perioderne 40 s og 3 s for punkt 1000CCX og perioden 20 s for punkt 1000EEX, hvilket kan indikere, at der muligvis er mindre harmoniske svingninger i forsøgsopstillingen. Da der ikke er observeret nogen svingning, som gentages i begge tidsserier, og da svingningerne desuden er forholdsvis små, er det vurderet, at det ikke er nødvendigt at medtage dem i modellen.