MIKE 11 modellering af sporstofforsøg
Formål
I dette afsnit er det forsøgt at modellere sporstofforsøget, som blev udført af projektgruppen i Østerå d. 09.09.04. Formålet med dette er at bestemme en dispersionskoefficient, der er repræsentativ for åen. Denne vil blive benyttet i en senere modellering af et forureningsscenario for Østerå. Modelleringen er udført i MIKE 11 med det modelopsæt, som senere er benyttet til at modellere åens iltforhold.
[ Tilbage]
Beregning af stoftransport og spredning
MIKE 11 benytter Fick´s 2. lov eller den generelle transport- dispersionsligning til at beregne stoftransporten. For en given vandløbsstrækning udtrykkes den som følgende.
![]() (1)
(1)
hvor
C er koncentrationen af stoffet [kg/m3]
A er tværsnitsarealet af vandløbet [m2]
t er tidsskridtet [s]
D er dispersionskoefficienten [m2/s]
Q er vandføringen [m3/s]
dx er stedsskridtet [m]
K er en 1. ordens
nedbrydningskonstant [s-1]
q er tilløb fra grundvand eller sidetilløb [m3/s]
C2 er koncentrationen af stof fra sidetilløb eller grundvandsindsivning [kg/m3]
Ligningen bygger på 2 transportmekanismer, henholdsvis transport med vandføringen, eller konvektiv transport, og transport på baggrund af koncentrationsgradienter af stoffet. Denne transport benævnes den dispersive transport.
Det forudsættes i beregningen, at stoffet er ligeligt fordelt over hele tværsnittet. I ovenstående ligning er det endvidere forudsat, at stoffet er konservativt eller udsat for nedbrydning ud fra en lineær nedbrydningskoefficient for stoffet [MIKE 11, 2004]
[ Til toppen] [ Tilbage]
Modelleringsresultater
Til at modellere sporstofforsøget er der som udgangspunkt benyttet samme modelopsæt, som der er benyttet ved modelleringen af iltforholdene på vandløbsstrækningen. Randbetingelserne i denne model stemmer overens med de målinger af vandstand og vandføring, som projektgruppen har udført på lokaliteten og er efterfølgende kalibreret på plads efter vanddybder målt på vandløbsstrækningen.
I modellen er stoffet tilført som en punktinjektion over et tidsskridt på ét sekund. Se Figur 1.
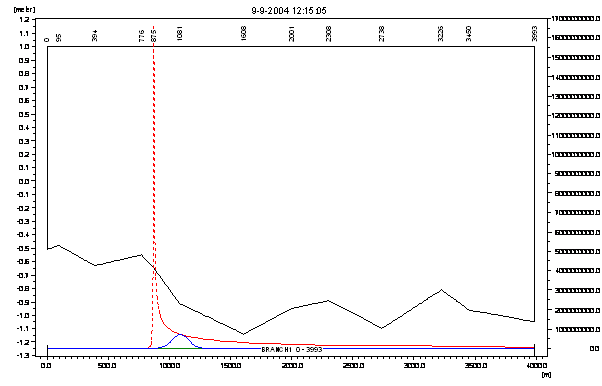
Figur 1 Blå kurve = stofkoncentration ca. 10 min. efter tilførslen. Sort kurve = bundkote i vandløbet. Rød stiplet kurve = Max stofkoncentration over hele modelleringsperioden.
I forsøget på at modellere sporstofforsøget er der i MIKE 11 indsat en tidsserie, som gengiver de målte millivolt værdier, der er moniteret under sporstofforsøget. Tidsserien er så benyttet som sammenligningsgrundlag 1100 meter nedstrøms injektionspunktet i modellen.
Umiddelbart er det ikke muligt at sammenligne resultat fra måling og modellering, eftersom de målte værdier er i millivolt og de modellerede værdier har en enhed i form af koncentration. Der er derfor lavet en massebetragtning, hvor arealet under dispersionskurverne er sammenlignet. Stemmer arealerne overens, kan det betragtes som et udtryk for at den tilførte masse af stof er ens under måling og modellering. Af denne grund er der ingen enheder på y aksen i de efterfølgende grafiske afbildninger.
Der er efterfølgende gennemført 2 modelleringer med den færdigkalibrerede strømningsmodel, hvor der er benyttet de to dispersionskoefficienter, som er beregnet ud fra det gennemførte sporstofforsøg. Disse er beregnet ud fra henholdsvis den observerede strømningshastighed og en gennemsnitshastighed for tværsnittet. Værdier ses i Tabel 1.
|
Metode |
x [m] |
v [m/s] |
D [m2/s] |
|
Tyngdepunkt |
1100 |
0,26 (obs) |
4,01 |
|
Tyngdepunkt |
1100 |
0,11 (gns) |
0,63 |
Tabel 1 Dispersionskoefficienter bestemt ved sporstofforsøg.
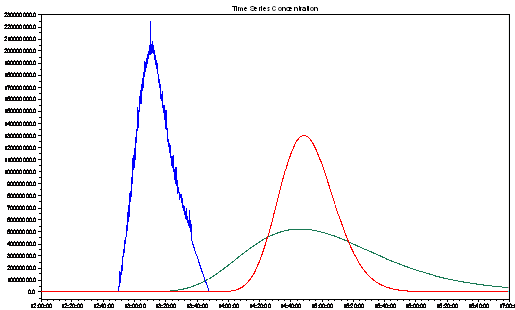
Resultatet af modelleringerne ses på Figur 2.
Figur
2
Modelleret og målt stofforløb 1100 meter
efter den momentane tilførsel. Blå kurve = målt stofforløb. Rød kurve = modelleret
stofforløb med D = 0,63 m2/s. Grøn kurve = modelleret stofforløb
med D = 4,01 m2/s.
Det ses på Figur 2 , at der er en forsinkelse i det modellerede stofforløb i forhold til det målte stofforløb på ca. 1,5 time. Dette skyldes, at stoffet i MIKE 11 transporteres med den samme hastighed i hele tværsnittet, eller noget der ligner den gennemsnitshastighed som projektgruppen har målt. Dette har ikke været tilfældet under sporstofforsøget, hvor stoffet sandsynligvis har befundet sig i midten af tværsnittet, hvor hastigheden er størst.
I forsøget på at få stofkurverne til at stemme tidsmæssigt overens har det været nødvendig at ændre på den færdigt kalibrerede strømningsmodel. Resultatet af kalibreringen ses i Tabel 2.
|
Model |
Hastighed v [m/s] |
Vanddybde [m] |
Manningtal [m1/3/s] |
Dispersionskoefficient [m2/s] |
|
Kalibreret strømningsmodel |
0,084 - 0,28 |
0,17 - 0,81 |
8,3 – 24,0 |
- |
|
Kalibreret stoftransportmodel |
0,17 - 0,51 |
-0,11 - 0,42 |
83,5 |
3,9 |
Tabel 2 Parameterværdier for strømningsmodel og stoftransportmodel
Det ses i Tabel 2 , at parametrene i den færdigkalibrerede stoftransportmodel afviger fra parametrene i strømningsmodellen. Det har været nødvendigt at sætte Manningtallet op til en urealistisk stor værdi. Et totalt grødefrit vandløb skulle ikke have et Manningtal større end 55 [Brorsen og Larsen, 2001] og Østerå vurderes at have en kraftig grødebevoksning. Det noteres desuden, at det høje Manningtal resulterer i negative vanddybder, hvilket selvfølgelig ikke er realistisk. De negative vanddybder skyldes ustabilitet i modellen ved at den låses fast med ét bestemt Manningtal samt én bestemt hældning på vandspejlet. Vandføringen er defineret på øvre rand og tværsnitaraalerne i modellen er defineret ud fra en implementeret vandløbsgeometri. Derfor kan modellen udelukkende respondere på det høje Manningtal ved at justere på vanddybden. Modellen håndterer negative vanddybder ud fra en defineret minimumsvanddybde, således at beregningen ikke går i stå ved udtørring [MIKE 11, 2004]. Udtørring i modellen påvirker derfor heller ikke stoftransporten.
Overensstemmelsen mellem det målte sporstofforløb og det modellerede stofforløb ses på Figur 3.
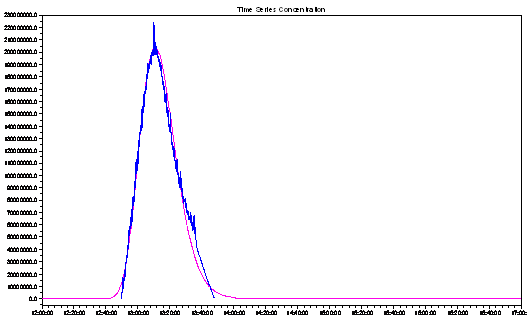
Figur 3 Resultat efter at strømningsmodellen er kalibreret ind efter den målte stoftransport. Blå kurve = målt stofforløb. Lilla kurve = modelleret stofforløb.
[ Til toppen] [ Tilbage]
Vurdering af stoftransportmodelleringen
Det har ikke været muligt at modellere det målte stoftransportforløb med den strømningsmodel, som er kalibreret ind efter de målte strømningsforhold. I forsøget på at kalibrere modellen ind efter stoftransporten er der benyttet urealistiske værdier for kalibreringsparametrene, hvilket resulterer i, at modellen ikke beskriver de aktuelle strømningsforhold, som den skal. Hovedproblemet har været, at stoffet under forsøget har bevæget sig med for stor hastighed i forhold til gennemsnitshastigheden i tværsnittet. Strømningsmodellen er kalibreret ind efter målte vandstande og har randbetingelser i form af bl.a. en målt vandføring. På den måde stemmer strømningshastigheden i modellen overens med de målte gennemsnitshastigheder.
Såfremt moniteringen af sporstoffet var foregået længere nedstrøms, således at stoffet havde fået længere tid til at blive opblandet i hele tværsnittet, er det muligt at måling og modellering havde stemt bedre overens. På den måde ville det også i større omfang have været muligt ved hjælp af MIKE 11 at finde en repræsentativ værdi for dispersionskoefficienten. Det er umiddelbart vurderet, at en éndimensional model som MIKE 11 i dette tilfælde er utilstrækkelig til at modellere de korrekte ilt og strømningsforhold samt den korrekte stoftransport på samme tid.
[ Til toppen] [ Tilbage]
Opsummering
Følgende dispersionskoefficienter er beregnet og modelleret, se Tabel 3.
|
Metode |
v [m/s] |
D [m2/s] |
|
Tyngdepunkt |
0,11 (gns) |
0,63 |
|
Tyngdepunkt |
0,26 (obs) |
4,01 |
|
MIKE 11 |
0,17 – 0,51 |
3,90 |
|
Analytisk |
0,27 |
4,76 |
Tabel 3 Beregnede og modellerede dispersionskoefficienter.
Det har ikke været muligt at finde en dispersionskoefficient, der med tilstrækkelig nøjagtighed gengiver det målte forløb i modellen. Det er derfor valgt at gennemføre den videre stofmodellering med både den mindste og den største værdi for D fra Tabel 3 og derpå sammenligne resultaterne. Dette interval svarer i rimelig grad til det interval, som de fleste dispersionskoefficienter for små vandløb ligger inden for. Her ligger værdien for D gerne mellem 1-5 m2/s [MIKE 11, 2004].
Et beregningsresultat på baggrund af dispersionsværdien 0,63 m2/s vil på den baggrund indgå som et ”worst case scenario”.
[ Til toppen] [ Tilbage]