|
|
| Figur 42 Placering af hastighedsprofiler udvalgt til hhv. kalibrering og validering. |
Ved anvendelse af Smagorinsky-modellen til modellering af turbulens, beregnes hvirvelviskositeten ud fra ændringer i hastighedsfeltet. Ved anvendelse af modellen er de såkaldte Smagorinsky konstanter til rådighed som kalibreringsparametre i hhv. horisontal og vertikal retning. Der er benyttet den beskrevne modelopsætning, og kalibrering og validering af modellen tager udgangspunkt i de udførte målinger af hastigheder med Laser Doppler anemometer. Som kalibrering og validering er der udvalgt otte hastighedsprofiler, som er beliggende hhv. 10 cm, 30 cm og 100 cm fra indløbet. På nedenstående figur ses området omkring indløbet i renden i xz-planen med placeringen af de valgte hastighedsprofiler.
|
|
| Figur 42 Placering af hastighedsprofiler udvalgt til hhv. kalibrering og validering. |
Kalibreringen gennemføres ved at justere de to Smagorinsky konstanter Csm
for hhv. horisontal og vertikal retning. Oftest skal den vertikale værdi være
større end den horisontale, for at sikre en større afhængighed i den vertikale
retning end i den horisontale.
[DHI, 2003]. Begge konstanter er justeret i intervallet 0,02 til
0,5.
Der er desuden kalibreret på slip-faktoren på bunden, som sættes til en værdi
mellem nul og en. I hvert af de fire kalibreringsprofiler er middelhastighederne i både x- og
z-retningen medtaget i vurderingen af resultatet.
I den kalibrerede model, er der anvendt værdier for Csm på 0,2 og 0,5 i hhv. horisontal og vertikal retning, samt en slip-faktor på bunden på 0,5.
Gennem kalibreringen er RMSE værdien, som er et udtryk for fejlen mellem målt og simuleret, søgt minimeret for hver enkelt profil. For den færdigkalibrerede model, er der angivet korrelationskoefficienter, r, som udtrykker kvaliteten af sammenhængen mellem de målte og simulerede data. Denne kan antage værdier mellem -1 og 1. Hvis den numeriske værdi ligger tæt på 1, er der en god overensstemmelse (korrelation) og ligger den numeriske værdi tæt på 0, er der en dårlig sammenhæng.
I nedenstående figurer, er de udvalgte hastighedsprofiler vist med målte og simulerede værdier med den færdigkalibrerede model. Det første kalibreringsprofil er beliggende 10 cm fra indløbet og 2 cm fra væggen inde i strålen.
|
|
|
| Figur 43 Målt og modelleret hastighedsprofil i st. 100BX med en korrelationskoefficient, r, på 0,96. Exelberegning. | Figur 44 Målt og modelleret hastighedsprofil i st. 100BZ med en korrelationskoefficient, r, på 0,74. Exelberegning. |
Her ses, hvordan de målte data i x-aksens retning ved bunden har tendens til at
tage form efter det logaritmiske hastighedsprofil, mens hastighederne falder
længere oppe i renden. Dette kan dels skyldes påvirkning fra væggene, og dels at
indløbet er placeret fra nul til 10 cm fra bunden, hvilket betyder at
hastigheden, som følge af strålen, er større nederst i profilet. De simulerede
hastigheder er ligeledes lave i toppen af profilet og stigende mod bunden, men
det er ikke muligt, at beskrive den logaritmiske form i den nederste del af
profilet. Hastighederne i z-aksens retning er meget lave, hvilket også er
tilfældet ved de simulerede værdier.
Det andet kalibreringsmål er også placeret 10 cm fra indløbet, men er i z-aksens retning valgt umiddelbart ved siden af indløbsstrålen, dvs. 14 cm fra kanten af renden.
|
|
|
| Figur 45 Målt og modelleret hastighedsprofil i st. 100EX med en korrelationskoefficient, r, på 0,50. Exelberegning. | Figur 46 Målt og modelleret hastighedsprofil i st. 100EZ med en korrelationskoefficient, r, på 0,47. Exelberegning. |
Her ses der i x-aksens retning negative hastigheder i de målte data i hele
profilet. Dvs. der sker strømning mod strømretningen. Dette sker, da der er så
stor hastighed i indløbsstrålen i forhold til den øvrige del af tværsnittet, at
der "suges" vand ind i strålen, og dermed mod strømretningen. Dette er også i
overensstemmelse med det, der blev observeret ved det udførte sporstofforsøg,
hvor der blev doseret en mængde rohdamin i indløbsstrålen.
Se video af forsøget. Det er i
modellen ikke muligt at opnå negative hastigheder i hele profilet. De målte
hastigheder i z-aksens retning er også her lave, hvilket i modellen ikke opnås i
hele profilet.
Det tredje kalibreringsmål er valgt 30 cm fra indløbet.
|
|
|
| Figur 47 Målt og modelleret hastighedsprofil i st. 300CX med en korrelationskoefficient, r, på 0,93. Exelberegning. | Figur 48 Målt og modelleret hastighedsprofil i st. 300CZ med en korrelationskoefficient, r, på 0,81. Exelberegning. |
Her ses igen samme tendens i de målte data, som det var tilfældet ved det første
kalibreringsprofil. Også her ses den samme tendens ved de simulerede værdier,
med lave værdier i toppen af profilet, og manglende evne til at beskrive det
logaritmiske hastighedsprofil ved bunden. I z-aksens retning, ses samme
variation i dybden, men hastighederne simuleres generelt for lave.
Det sidste profil er valgt 100 cm fra indløbet, hvor der igen ses samme tendens som i det første og det tredje profil med hensyn til hastighederne i x-aksens retning. Dog er hastighederne mindre som følge af den større afstand til indløbet. Det er muligt at simulere de observerede værdier, igen med undtagelse af den nederste del af profilet, hvor det logaritmiske profil ikke kan beskrives i modellen. I z-aksens retning er der i modsætning til det forrige profil tendens til at overestimere hastighederne.
|
|
|
| Figur 49 Målt og modelleret hastighedsprofil i st. 1000DX med en korrelationskoefficient, r, på 0,93. Exelberegning. | Figur 50 Målt og modelleret hastighedsprofil i st. 1000DZ med en korrelationskoefficient, r, på 0,27. Exelberegning. |
Der er en generel tendens til, at der er en bedre sammenhæng mellem målte og
simulerede hastigheder i x-aksens retning end i z-aksens retning, udtrykt ved de
beregnede korrelationskoefficienter. Med henblik på en senere sammenligning med
valideringsresultatet, er middelkorrelationskoefficienten beregnet til 0,70.
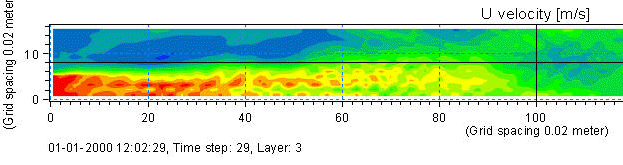
Der er lavet en animation af kalibreringsresultatet, der illustrerer, hvordan strømningen foregår ned gennem renden. Der er vist resultatet i en afstand på 5 cm fra bunden. Se animation her. På nedenstående figur ses et billede af hastighederne ved indløbsstrålen. Her ses, hvordan der opstår negative hastigheder ved siden af indløbsstrålen, og der er et stagnationspunkt omkring 1,2 m fra indløbet.
 |
|
| Figur 51 Hastigheder ved indløbsstrålen vist i en afstand af 5 cm fra bunden. Se animation her. | |
Valideringen af modellen er sket ved at vælge fire målte hastighedsprofiler, som sammenlignes med simulerede profiler beregnet med den kalibrerede model. Der er valgt profiler beliggende i samme afstand fra indløbet som ved kalibreringen, dvs. i 10 cm, 30 cm og 100 cm. Profilerne er derimod placeret i en anden afstand fra væggen end de fire anvendt ved kalibreringen, det er således fire profiler, der er uafhængige af kalibreringsmålene. I nedenstående figurere ses resultatet af valideringen.
|
|
|
| Figur 52 Målt og modelleret hastighedsprofil i st. 100CX med en korrelationskoefficient, r, på 0,95. Exelberegning. | Figur 53 Målt og modelleret hastighedsprofil i st. 100DCZ med en korrelationskoefficient, r, på 0,80. Exelberegning. |
|
|
|
| Figur 54 Målt og modelleret hastighedsprofil i st. 100DX med en korrelationskoefficient, r, på 0,97. Exelberegning. | Figur 55 Målt og modelleret hastighedsprofil i st. 100DZ med en korrelationskoefficient, r, på 0,28. Exelberegning. |
|
|
|
| Figur 56 Målt og modelleret hastighedsprofil i st. 300DX med en korrelationskoefficient, r, på 0,87. Exelberegning. | Figur 57 Målt og modelleret hastighedsprofil i st. 300DZ med en korrelationskoefficient, r, på 0,63. Exelberegning. |
|
|
|
| Figur 58 Målt og modelleret hastighedsprofil i st. 1000CX med en korrelationskoefficient, r, på 0,79. Exelberegning. | Figur 59 Målt og modelleret hastighedsprofil i st. 1000CZ med en korrelationskoefficient, r, på 0,29. Exelberegning. |
Betragtes de viste figurer og de beregnede korrelationskoefficienter ses, at der i validering er samme tendenser, og generelt samme evne til at simulere de målte hastigheder. Der er beregnet en middel korrelationskoefficient for valideringen på 0,69, hvor der til sammenligning blev beregnet en værdi for kalibreringen på 0,70. En mindre korrelation for valideringen end for kalibreringen kan accepteres, og må, afhængig af hvor god en kalibrering der er gennemført, også forventes. Hvis valideringen derimod havde givet bedre resultater end kalibreringen antyder det, at kalibreringsprocessen endnu ikke er færdig, og at modellen kan kalibreres til et bedre resultat.
Som en del af vurderingen af kalibrerings- og valideringsresultatet skal det også nævnes, at der har været flere målte hastighedsprofiler til rådighed, end der har været anvendt i hhv. kalibrering og validering. Af hensyn til tiden, der har været til rådighed, er der derfor udvalgt en række målinger til at indgå i vurderingen af kalibreringen og valideringen. Det er muligt, at der ved anvendelse af andre eller flere hastighedsprofiler end de her udvalgte, kan opnås et andet kalibrerings- og valideringsresultat. Det er dog vurderet, at modelleringsresultatet fremkommet med modellen kalibreret med de her udvalgte hastighedsprofiler, ikke vil variere betydeligt fra en model kalibreret med andre eller flere af de målte hastighedsprofiler, pga. fordelingen af de anvendte hastighedsprofiler over hele området omkring indløbsstrålen. Der ses desuden, at mange af de målte hastighedsprofiler i større eller mindre grad er sammenlignelige i de enkelte tværsnit, hvilket også vil bevirke, at anvendelsen af andre hastighedsprofiler vil få mindre betydning.
En anden faktor, der kan have betydning for, hvor god en kalibrering og validering der kan gennemføres, er muligheden for, at der i de målte data ligger svingninger eller spring i datasættet, som ikke umiddelbart medtages i modellen. Dette kan eksempelvis være fra egen-svingninger i renden eller ustabilitet i pumpen. Dette er undersøgt gennem en kvalitetskontrol i form af en tidsserieanalyse af enkelte af de målte datasæt, hvor der bl.a. er undersøgt for spring i datasættet, som kan få betydning for den målte middelhastighed. Der er desuden gennemført en spektralanalyse, hvor variansspektret er opstillet for de udvalgte tidsserier. Undersøgelserne har ikke vist nogen anormaliteter i de anvendte data, og der er umiddelbart ikke fundet svingninger, der kan få betydning for kalibreringen og valideringen af modellen.
Det er vurderet, at det vil være muligt at finjustere kalibreringen evt. med et
bedre kalibrerings- og valideringsresultat til følge, såfremt der vil være mere
tid til rådighed til kalibreringsprocessen, dog accepteres valideringen af modellen
på baggrund af ovenstående, med udgangspunkt i den tid der har været til
rådighed for kalibreringsprocessen.