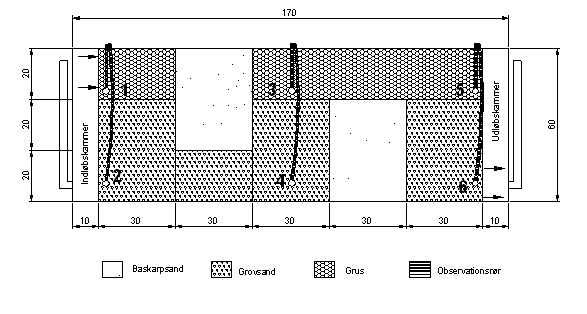
Vandtransportmodel
Formål
For beregning af vandtransporten i sandkassen er der lavet en boksmodel. Formålet med boksmodellen er at beskrive vandtransporten i sandkassen. Herudover er formålet, at bestemme den hydrauliske ledningsevne for henholdsvis grus, grovsand og baskarpsand gennem kalibrering ud fra målte trykniveauer og flow.
Modellen er 2-dimensional og opbygget i programmet Matlab.
Opbygningen af modellen
I det følgende er opbygningen af modellen og de styrende ligninger beskrevet.
Diskretisering
Sandkassen har en længde på 150 cm og en højde på 60 cm. Diskretiseringen af sandkassen er udført med en værdi på 2 cm i henholdsvis vertikal og horisontal retning. Det betyder, at sandkassen er opdelt i 2250 kvadratiske bokse. Diskretiseringen af sandkassen ses på Figur 1.
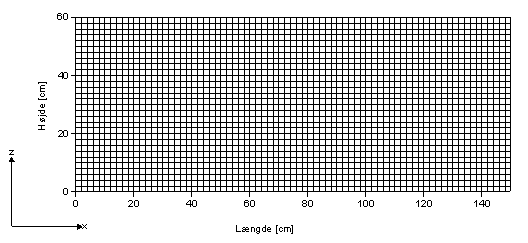
Figur 1 Diskretisering af sandkassen.
Der er frit vandspejle i sandkassen. Herudover er sandkassen åben i højden 40-60 cm i venstresiden og 0-20 cm i højresiden.
Nulpunktet i modellen er sat til det nederste hjørne i venstreside af sandkassen.
Massebalance for boksene
For hver enkelt boks er massebalancen opstillet. Massebalancen for boks I,J er angivet på Figur 2 og nedenstående.
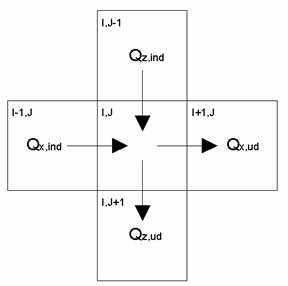
Figur 2 Massebalance for boks I,J.
Massebalancen for boks I,J er på Figur 2 angivet som flowet ind i boksen minus flowet ud af boksen. Opskrevet som ligning ser massebalancen for boks I,J ud som nedenstående.
![]() (1)
(1)
hvor
hI,J er trykniveauet i boksen [m]
Δt er tidsskridtet [s]
Δy er dybden af boksen [m]
Δx er længden af boksen [m]
SI,J er magasintallet [-]
Qx,ind er det horisontale flow ind i boksen [m3/s]
Qx,ud er det horisontale flow ud af boksen [m3/s]
Qz,ind er det vertikale flow ind i boksen [m3/s]
Qz,ud er det vertikale flow ud af boksen [m3/s]
Der er kun regnet med stationære forhold i modellen, hvilket betyder, at venstresiden i ligning 1 er lig 0. Dermed er ligningen for massebalancen opskrevet som nedenstående.
![]() (2)
(2)
Flowberegninger
De enkelte flow i massebalanceligningen er beregnet af Darcy hastigheden og det gennemstrømmede areal som nedenstående.
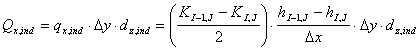 (3)
(3)
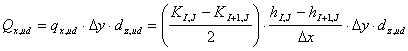 (4)
(4)
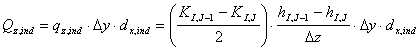 (5)
(5)
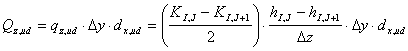 (6)
(6)
hvor
q er Darcy hastigheden [m/s]
dz er den gennemstrømmede højde på kanten af boksen [m]
dx er den gennemstrømmede bredde på kanten af boksen [m]
Δz er højden af boksen [m]
K er den hydrauliske ledningsevne [m/s]
Den gennemstrømmede højde
Den gennemstrømmede højde er indført, da de øverste bokse i modellen ikke er vandfyldte og vandtransporten derfor ikke foregår i hele boksenes højde.
Den gennemstrømmede højde på kanterne af boksene er bestemt af trykniveauerne i boksene, som netop angiver vandstanden i boksene. Bestemmelsen af den gennemstrømmede højde er foregået efter følgende ligninger.
![]() (7)
(7)
![]() (8)
(8)
hvor
Hnedre er koten for undersiden af boksen [m]
Iterativ beregning af trykniveauer
Trykniveauet i boks I,J er beregnet ved at indsætte ligning 3, 4, 5 og 6 i ligning 2, hvorved nedenstående ligning er fremkommet.
![]() (9)
(9)
hvor
![]()
![]()
![]()
![]()
n er iterationstrinet [-]
Ligning 9 er løst iterativt med Jacobi metoden. Hermed er beregningen af det nye trykniveau foregået med 4 trykniveauer fra det forrige iterationstrin.
Initialbetingelser
Normalt gælder det, at valget af initialbetingelser er af mindre betydning, når der er tale om iterative beregningsprocesser. Vælges initialbetingelserne med stor afvigelse fra beregningsresultaterne, øges det nødvendige antal iterationstrin blot. Et øget antal iterationstrin medfører længere beregningstid.
I nærværende model er trykniveauerne anvendt som initialbetingelser. Valget af initialbetingelser har ikke været helt ligegyldigt. Er trykniveauer valgt for lave i toppen af sandkassen, er store dele af modellen udtørret og beregningen er gået i stå.
For at undgå unødig udtørring af modellen er initialtrykniveauerne valgt en hel del større end beregningsresultaterne i toppen af sandkassen. Dette har medført, at der er foretaget mange iterationstrin før, at der er opnået konvergens. Initialbetingelserne ses på Figur 3.
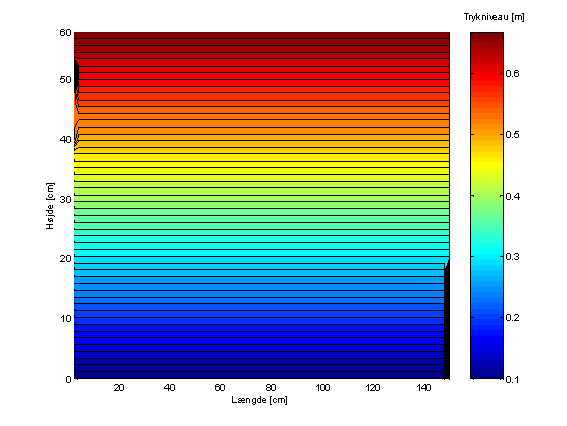
Figur 3 Initialbetingelse. Trykniveauer [m].
Randbetingelser
Randbetingelserne i modellen består af trykniveauerne i observationsrør 1 og 6 ved den åbne del af sandkassen i venstre- og højresiden.
Konvergenskriterium
For at bestemme, hvornår modellen konvergerer, er der opsat et konvergenskriterium. Konvergenskriteriet er opfyldt, når summen af de absolutte trykændringer mellem to iterationstrin er mindre end 0,1 mm. Når konvergenskriteriet er opnået, er beregningen afsluttet.
Kontrol af modellen
For at undersøge om modellen regner korrekt er der indsat to strømningstilfælde i modellen, hvor resultatet på forhånd er kendt. I begge strømningstilfælde er den hydrauliske ledningsevne konstant i hele sandkassen.
Strømningstilfælde 1
I strømningstilfælde 1 er hele sandkassens venstre- og højreside åben. Trykniveauet på hele venstresiden er sat til 0,65 m mens det på hele højresiden er sat til 0,62 m. Da trykket på hele venstre- og højresiden er over sandkassens højde, er ingen af boksene udtørret. Hermed er det undersøgt, om modellen behandler Darcy’s lov korrekt. På Figur 4 ses resultatet af modelleringen.
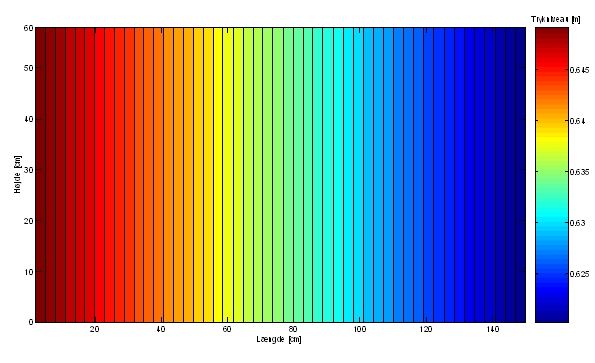
Figur 4 Resultat af modellering af strømningstilfælde 1.
Figur 4 viser ud fra den konstante afstand mellem konturlinierne, at trykniveauet falder lineært fra randbetingelsen på 0,65 m i kassens venstreside til randbetingelsen på 0,62 m i kassens højreside. Dette indikerer, at modellen behandler Darcy’s lov korrekt.
Den hydrauliske ledningsevne er i hele sandkassen sat til 6,94∙10-4 m/s. Med kendskab til den hydrauliske ledningsevne og trykniveauerne i både venstre- og højresiden er flowet ud af sandkassen beregnet til 3,33∙10-6 m3/s med Darcy’s lov. Med modellen er flowet beregnet til 3,33∙10-6 m3/s. Dermed er det konkluderet, at modellen behandler Darcy’s lov korrekt.
Strømningstilfælde 2
I strømningstilfælde 2 er trykniveauet på hele venstresiden sat til 0,50 m mens det på hele højresiden er sat til 0,15 m. Det betyder, at store dele af sandkassen er udtørret. Hermed er det undersøgt, om modellen behandler Darcy’s lov korrekt samtidig med, at den inaktiverer udtørrede bokse. Resultatet af modelleringen ses på Figur 5.
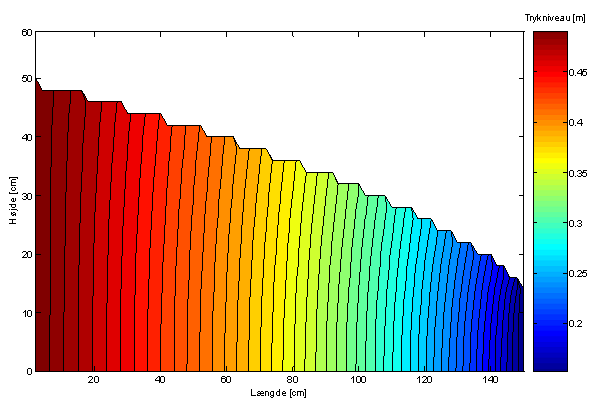
Figur 5 Resultat af modellering af strømningstilfælde 2.
På Figur 5 ses det, at trykgradienten stiger fra randbetingelsen på 0,5 m i sandkassens venstreside til randbetingelsen på 0,15 m i sandkassens højreside. Dette er et udtryk for, at den samme mængde vand skal passere et aftagende strømningsareal.
For at undersøge om modellen behandler vandtransporten korrekt, er indløbsflowet i sandkassen sammenlignet med flowet ud af sandkassen. Både ind- og udløbsflowet er på 2,13∙10-5 m3/s, hvilket betyder, at modellen beskriver transporten korrekt.
Kalibrering
Som beskrevet tidligere er formålet med modellen at beskrive vandtransporten i sandkassen samt at bestemme den hydrauliske ledningsevne for grus, grovsand og baskarpsand. Dette er gjort ved, at anvende de hydrauliske ledningevner som kalibreringsparametre. Fordelingen af de tre jordtyper i sandkassen er angivet på Figur 6.
Figur 6 Fordeling af de 3 jordtyper i sandkassen.
Startværdierne for de hydrauliske ledningsevner er bestemt af kornkurverne for de 3 jordtyper. For bestemmelsen se HER. Værdierne ses også i Tabel 1 .
|
|
Baskarpsand |
Grovsand |
Grus |
|
Kstart [m/s] |
7,2.10-5 |
9,0.10-4 |
1, 3.10-2 |
Tabel 1 Startværdier for kalibreringsparametrene.
Modellen er kalibreret i forhold til trykniveauer aflæst i observationsrør 2, 3, 4 og 5 samt det målte flow ud af sandkassen. Trykniveauerne i observationsrør 1 og 6 er anvendt som randbetingelser. Værdierne for flowet og trykniveauerne ses i Tabel 2.
|
|
Målte/aflæste værdier |
|
Trykniveau i observationsrør 1 |
0,536 m |
|
Trykniveau i observationsrør 2 |
0,520 m |
|
Trykniveau i observationsrør 3 |
0,486 m |
|
Trykniveau i observationsrør 4 |
0,499 m |
|
Trykniveau i observationsrør 5 |
0,486 m |
|
Trykniveau i observationsrør 6 |
0,463 m |
|
Flow ud af sandkassen |
3,5.10-6 m3/s |
Tabel 2 Kalibreringsværdier.
For kalibreringen og den senere validering af modellen er der bestemt nogle afvigelseskriterier, som afvigelsen mellem de modellerede værdier og kalibrerings/valideringsværdierne ikke bør overstige.
Afvigelseskriteriet for trykniveauerne er bestemt ud fra usikkerheden ved aflæsningerne af trykniveauerne i observationrørerne. Usikkerheden er vurderet til ca. 2 mm.
For flowet ud af kassen er afvigelseskriteriet bestemt ud fra usikkerheden i målingerne af flowet. Der er til hver bestemmelse af flowet udført 3 målinger. I alt er flowet bestemt for 6 strømningstilfælde. Af disse 6 strømningstilfælde er afvigelseskriteriet bestemt som den største værdi beregnet med nedenstående ligning.
![]() (10)
(10)
hvor
i er strømningstilfældet [-]
mi,max er det største flow, som er målt for strømningstilfældet [m3/s]
mi,min er det mindste flow, som er målt for strømningstilfældet [m3/s]
mi,middel er middelflowet i strømningstilfældet [m3/s]
Afvigelseskriteriet for flowet er af ovenstående beregnet til 5 % af middelflowet i det betragtede strømningstilfælde.
Som start på kalibreringen er der gennemført en modellering med startværdierne for de hydrauliske ledningsevner. Nedenstående på Figur 7 ses resultatet af modelleringen med startværdierne.
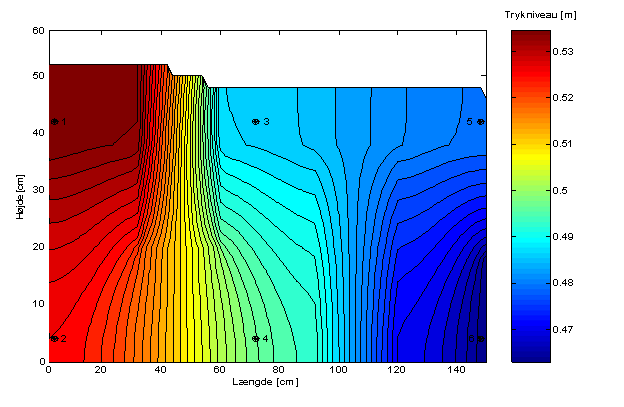
Figur 7 Resultat af modellering med startværdierne for den hydrauliske ledningsevne samt placeringen af observationsrørerne.
I Tabel 3 ses de modellerede trykniveauer og flowet i forhold til kalibreringsværdierne.
|
|
Målte/aflæste værdier |
Modellerede værdier |
Afvigelse |
Afvigelses-kriterium |
Afvigelse fra kriterium |
|
Trykniveau i obs.rør 2 |
0,520 m |
0,526 |
6 mm |
2 mm |
200 % |
|
Trykniveau i obs.rør 3 |
0,486 m |
0,487 |
1 mm |
2 mm |
- |
|
Trykniveau i obs.rør 4 |
0,499 m |
0,497 |
2 mm |
2 mm |
- |
|
Trykniveau i obs.rør 5 |
0,486 m |
0,480 |
6 mm |
2 mm |
200 % |
|
Flow ud af sandkassen |
3,5.10-6 m3/s |
3,51.10-6 m3/s |
8,2.10-9
m3/s |
1,8.10-7 m3/s |
- |
Tabel 3 Modellerede værdier med startværdierne for de hydrauliske ledningsevner i forhold til kalibreringsværdierne.
Figur 7 og Tabel 3 viser generelt, at modelleringen med startværdierne for de hydrauliske ledningsevner ikke har medført store afvigelser i mellem kalibreringsværdierne og de modellerede værdier. Det er kun afvigelserne mellem trykniveauer i observationsrør 2 og 5, som er større end afvigelseskriteriet.
I Tabel 4 ses de færdigt kalibrerede hydrauliske ledningsevner og startværdierne samt afvigelserne mellem dem.
|
|
Baskarpsand |
Grovsand |
Grus |
|
Kstart [m/s] |
7,2.10-5 |
9,0.10-4 |
1, 3.10-2 |
|
Kkal [m/s] |
1,0.10-4 |
8,1.10-4 |
6,9.10-2 |
|
Ændring [%] |
39 |
10 |
431 |
Tabel 4 Kalibrerede hydrauliske ledningsevner.
Det ses af Tabel 4, at den kalibrerede hydrauliske ledningsevne for baskarpsand og grus er højere end startværdien mens den for grovsandet er lavere.
Den kalibrede hydrauliske ledningsevne for gruset er mere end 4 gange større end startværdien. Dette skyldes, at der mellem kalibreringsværdien for trykniveauet i observationsrør 3 og 5, som ligger i gruset, ikke er nogen trykgradient. Det har derfor her været nødvendigt med en høj hydraulisk ledningsevne for ikke at få for store afvigelser mellem de aflæste og modellerede trykniveauer.
Resultatet af modelleringen med de kalibrerede hydrauliske ledningsevner ses nedenstående på Figur 8 og i Tabel 5 .
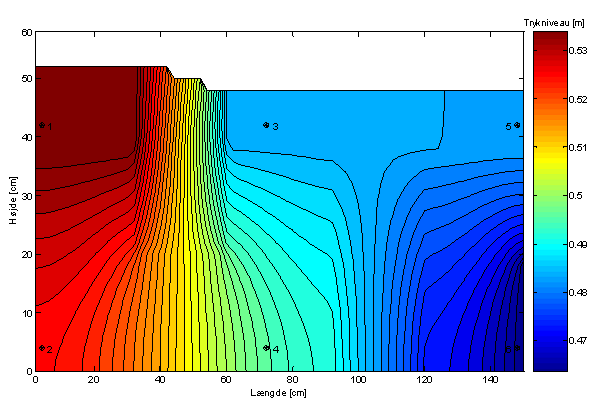
Figur 8 Kalibreringsresultat samt placeringen af observationsrørerne.
|
|
Målte/aflæste værdier |
Modellerede værdier |
Afvigelse |
Afvigelses-kriterium |
Afvigelse fra kriterium |
|
Trykniveau i obs.rør 2 |
0,520 m |
0,526 m |
6 mm |
2 mm |
200 % |
|
Trykniveau i obs.rør 3 |
0,486 m |
0,485 m |
1 mm |
2 mm |
- |
|
Trykniveau i obs.rør 4 |
0,499 m |
0,496 m |
3 mm |
2 mm |
100 % |
|
Trykniveau i obs.rør 5 |
0,486 m |
0,484 m |
2 mm |
2 mm |
- |
|
Flow ud af sandkassen |
3,5.10-6 m3/s |
3,76.10-6 m3/s |
2,6.10-7 m3/s |
1,8.10-7 m3/s |
44 % |
Tabel 5 Modellerede værdier med de kalibrerede hydrauliske ledningsevner i forhold til kalibreringsværdierne.
Det fremgår af Figur 8 og Tabel 5, at der på trods af kalibreringen af modellen med hensyn til de hydrauliske ledningsevner stadig er stor forskel mellem det aflæste og modellerede trykniveau i observationsrør 2. Det har ikke været muligt at mindske denne forskel.
Det fremgår herudover, at forskellen mellem kalibreringsværdien og modelleringsværdien i observationsrør 5 er mindsket betydeligt med kalibreringen, så afvigelsen ligger indenfor afvigelseskriteriet. Forskellen mellem kalibreringstrykniveauet og det modellerede trykniveau i observationsrør 4 er øget med kalibreringen, så afvigelsen ligger udenfor afvigelseskriteriet.
Med hensyn til flowet ud af sandkassen er afvigelsen mellem det målte og modellerede flow øget med kalibreringen i forhold til modelleringen med startværdierne. Afvigelsen er nu større end afvigelseskriteriet for flowet.
Det kan af det ovenstående diskuteres, om de kalibrerede hydrauliske ledningsevner er mere korrekte end startværdierne. Modelleringen med startværdierne har medført store afvigelser på trykniveauer i observationsrør 2 og 5. Modelleringen med de kalibrerede værdier har medført mindre afvigelser på trykniveauerne men også afvigelse på flowet.
I det følgende er det valgt at validere modellen ved modellering med både startværdierne og de kalibrerede hydrauliske ledningsevner.
Validering
Modellen er valideret i forhold til trykniveauer aflæst i observationsrør 2, 3, 4 og 5 samt det målte flow ud af sandkassen. Trykniveauerne i observationsrør 1 og 6 er anvendt som randbetingelser. Værdierne for trykniveauerne og flowet ses i Tabel 6.
|
|
Målte/aflæste værdier |
|
Trykniveau i observationsrør 1 |
0,525 m |
|
Trykniveau i observationsrør 2 |
0,498 m |
|
Trykniveau i observationsrør 3 |
- m |
|
Trykniveau i observationsrør 4 |
0,440 m |
|
Trykniveau i observationsrør 5 |
- m |
|
Trykniveau i observationsrør 6 |
0,351 m |
|
Flow ud af sandkassen |
8,0.10-6 m3/s |
Tabel 6 Valideringsværdier.
Som det fremgår af Tabel 6 er der ingen valideringsværdier for trykniveauerne i observationsrør 3 og 5. Dette skyldes, at sandkassen er tørlagt, hvor observationsrørerne er placeret.
Valideringsresultatet af modelleringen med startværdierne ses nedenstående på Figur 9 og i Tabel 7.
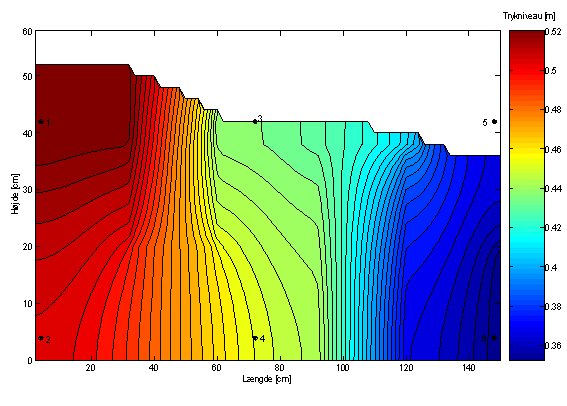
Figur 9 Valideringsresultat med startværdierne samt placering af observationsrørerne.
|
|
Målte/aflæste værdier |
Modellerede værdier |
Afvigelse |
Afvigelses-kriterium |
Afvigelse fra kriterium |
|
Trykniveau i obs.rør 2 |
0,498 m |
0,506 m |
8 mm |
2 mm |
300 % |
|
Trykniveau i obs.rør 3 |
- m |
0,437 m |
- mm |
2 mm |
- |
|
Trykniveau i obs.rør 4 |
0,440 m |
0,454 m |
14 mm |
2 mm |
600 % |
|
Trykniveau i obs.rør 5 |
- m |
- m |
- mm |
2 mm |
- |
|
Flow ud af sandkassen |
8,0.10-6 m3/s |
6,6.10-6 m3/s |
1,4.10-6 m3/s |
4.10-7 m3/s |
250 % |
Tabel 7 Modellerede værdier med startværdierne for de hydrauliske ledningsevner i forhold til valideringsværdierne.
Det ses af Figur 9 og Tabel 7, at valideringsresultatet ved modellering med startværdierne for de hydrauliske ledningsevner ligger langt fra valideringsværdierne. Herudover ses det, at boksen svarende til placeringen af observationsrør 3 ikke er udtørret i modelleringen.
Valideringsresultatet af modelleringen med de kalibrerede hydrauliske ledningsevner ses nedenstående på Figur 10 og i Tabel 8.
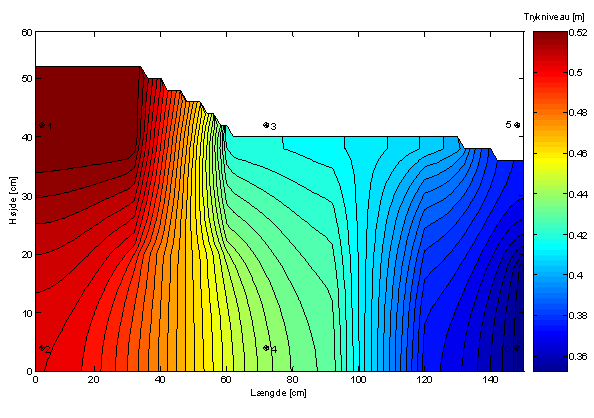
Figur 10 Valideringsresultat med de kalibrerede værdier for de hydrauliske ledningsevner samt placering af observationsrørerne.
|
|
Målte/aflæste værdier |
Modellerede værdier |
Afvigelse |
Afvigelses-kriterium |
Afvigelse fra kriterium |
|
Trykniveau i obs.rør 2 |
0,498 m |
0,504m |
6 mm |
2 mm |
200 % |
|
Trykniveau i obs.rør 3 |
- m |
- m |
- mm |
2 mm |
- |
|
Trykniveau i obs.rør 4 |
0,440 m |
0,441m |
1 mm |
2 mm |
- |
|
Trykniveau i obs.rør 5 |
- m |
- m |
- mm |
2 mm |
- |
|
Flow ud af sandkassen |
8,0.10-6 m3/s |
8,2.10-6 m3/s |
2.10-7 m3/s |
4.10-7 m3/s |
- |
Tabel 8 Modellerede værdier med de kalibrerede hydrauliske ledningsevner i forhold til valideringsværdierne.
Det ses af Figur 10 og Tabel 8, at afvigelsen mellem valideringsværdien og den modellerede værdi for trykniveauet i observationsrør 2 ligger over afvigelseskriteriet. Dette var også forventet, da det samme gjorde sig gældende i kalibreringen. Det ses herudover, at afvigelsen mellem valideringsværdien og den modellerede værdi for trykniveauet i observationsrør 4 og flowet ud af sandkassen ligger indenfor afvigelseskriteriet.
De to ovenstående valideringer viser, at modelleringen med de kalibrerede hydrauliske ledningsevner giver mindst afvigelse mellem valideringsværdierne og de modellerede værdier. Derfor er det vurderet, at disse værdier ligger tættest på de faktiske hydrauliske ledningsevner for de 3 jordtyper i sandkassen.
Sammenfatning
Af ovenstående fremgår det, at det ikke har været muligt at bestemme de hydrauliske ledningsevner entydigt for henholdsvis baskarpsand, grovsand og grus gennem kalibrering af modellen. Dette ses ved, at der ikke er opnået kalibreringsresultater, hvor samtlige afvigelser mellem kalibreringsværdierne og modelleringsværdierne ligger indenfor afvigelseskriterierne. Derimod er der fundet to forskellige kombinationer af hydrauliske ledningsevner, hvor afvigelserne mellem model- og kalibreringsværdierne er stort set lige store.
I det følgende er der givet bud på, hvad der forårsager fejl i modellen og dermed kan være medvirkende til, at der ikke er opnået tilfredsstillende resultater.
Diskretiseringsfejl
I vandtransportmodellen er der numeriske fejl med hensyn til den iterative løsning og diskretiseringsgraden. Disse fejl vil altid opstå ved numeriske løsninger [Henriksen et al., 2001]. Fejlenes indflydelse på resultaterne i modellen er nedenstående vurderet.
I forbindelse med den anvendte iterative løsning er der, som tidligere beskrevet, opsat et konvergenskriterium. Konvergenskriteriet udtrykker den ændring eller fejl, som maksimalt må være mellem to iterationstrin. Konvergenskriteriet er her defineret som summen af de absolutte trykændringer mellem to iterationstrin og er på 0,1 mm. Hvis alle bokse i modellen er aktiv, er modellen betragtet som konvergeret, når den gennemsnitlige trykændring i boksene er på 4,4.10-5 mm. Er én eller flere af boksene i modellen inaktive er konvergenskriteriet slækket, da den gennemsnitlige trykændring pr. boks mellem to iterationstrin herved er større end 4,4.10-5 mm.
Ovenstående betyder, at konvergenskriteriet er ”hårdere” for kalibrering af modellen end konvergenskriteriet for valideringen, da der er udtørret flest bokse i valideringen af modellen. Denne fejl og fejlen ved at sætte konvergenskriteriet større end nul er vurderet til at kunne negligeres i forhold øvrige fejl i modellen.
Diskretiseringen af sandkassen er udført med hensyn til 0,02 m i både horisontal og vertikalretning. En finere diskretisering på for eksempel 0,01 m kan måske afhjælpe en del af afvigelserne i mellem de målte og modellerede værdier. Det er ikke forsøgt, at modellere med en finere diskretisering, da beregningstiden herved øges betydeligt.
Entydighed
Entydigheden for modellen er ikke undersøgt. En nærmere undersøgelse af denne ville formentligt vise, at der ikke er entydighed i modellen. Dette medfører, at flere forskellige kombinationer af hydrauliske ledningsevne for de 3 jordtyper kan føre til samme kalibreringsresultat. Hermed kan ikke gives et entydigt resultat for de 3 hydrauliske ledningsevner.
Problemet omkring entydighed eller mangel på samme menes at være hovedårsagen til, at det ikke har været muligt at bestemme de hydrauliske ledningsevner gennem kalibrering.
Det er hermed konkluderet, at det ikke har været muligt med denne model at modellere de observerede forhold på tilfredsstillende vis.
De målte og kalibrerede hydrauliske ledningsevner for de 3 jordtyper er sammenlignet ved modellering i GMS, se nærmere HER.